From Jackknife to A/B Testing

Posted on 2019-12-23 22:28:32 +0900 in Data Science Jackknife Math A/B Testing

Background

In A/B Testing, there is a group of data $X = (X_1, X_2, ..., X_n)$ and $Y = (Y_1, Y-2, ..., Y_m)$ , the metrics we interested in are the difference between these two groups and related confidence.

A Quick Introduction to Jackknife

Jackknife is a method of resample, which tries to estimate the bias and variability of an estimator $\phi_n(X_1, X_2, ..., X_n)$ by using values of $\phi_n(X)$ on subsamples from $X_1, X_2, ..., X_n$ .

The $i^{th}$ pseudovalue of $\phi_n(X)$ is $ps_i(X) = n\phi_n(X_1, X_2, ..., X_n) - (n - 1)\phi_{n - 1}((X_1, X_2, ..., X_n)_{[i]})$ , where $X_{i}$ means the sample $X_1, X_2, ..., X_n$ with $i^{th}$ value $X_i$ deleted from the sample.

Treat the pseudovalue $ps_i(X)$ as if they were independent random variables with mean $\theta$ , then the confidence interval could be obtained using Central Limit Theorem. Specifically, let

$ps(X) = \frac{1}{n}\sum_{i=1}^{n}ps_i(X)$ and $V_{ps}(X) = \frac{1}{n - 1}sum_{i=1}^{n - 1}(ps_i(X) - ps(X))^2$

be the mean and sample variance of the pseudovalues. The jackknife 95% confidence interval is

$ps(X) - 1.96\sqrt{\frac{1}{n}V_{ps}(X)}, ps(X) + 1.96\sqrt{\frac{1}{n}V_{ps}(X)}$

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math

sample_count = 500000
K = 5000
mu, sigma = 500, 100 # mean and standard deviation

def jackknife_sder(s):

    df = pd.DataFrame(data = s, columns=['data'])
    groups = int(sample_count / K )
    def label_race (row):
        return int(row.name) % groups
    df['group'] = df.apply(lambda row: label_race(row), axis=1)

    average = df['data'].mean()

    total_sum = s.sum()
    left_k_groups = [(total_sum - (df['data'][df['group'] == x]).sum()) / (sample_count - K) for x in range(groups)]
    a = groups * average
    b = [v * (groups - 1) for v in left_k_groups]
    ps = a - b 
    
    mean, var = ps.mean(), (ps.var(ddof = 1.0) / groups) ** 0.5
    return mean, var

data = [np.random.normal(mu, sigma, sample_count) for i in range(100)]
s_vars = [jackknife_sder(d) for d in data]
s_mean, s_var =  mu, sigma / (sample_count ** 0.5)

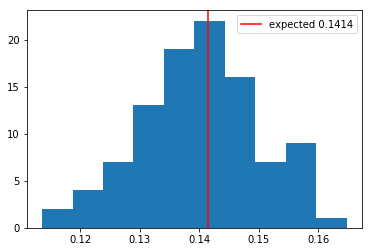
plt.hist(s_vars, bins=10)
plt.axvline(x=s_var, color='r', label=f'expected {s_var:.4f}')
plt.legend()
plt.show()

png

confidence = 1.96
l, r = (s_mean - confidence *  s_vars, s_mean + confidence *  s_vars)
print(f'left: {l:.4f}, right: {r:.4f}')

left: 499.7084, right: 500.2740

----------------------------------- 本文内容遵从CC版权协议转载请注明出自kamelzcs -----------------------------------

Monads »

From Jackknife to A/B Testing

Posted on 2019-12-23 22:28:32 +0900 in Data Science Jackknife Math A/B Testing

Background

A Quick Introduction to Jackknife

Hide Comments